Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts

Given a rectangular cake with height h and width w, and two arrays of integers horizontalCuts and verticalCuts where horizontalCuts[i] is the distance from the top of the rectangular cake to the i-th horizontal cut and similarly, verticalCuts[j] is the distance from the left of the rectangular cake to the j-th vertical cut.

Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a huge number, return this modulo $10^9 + 7$.

Example 1

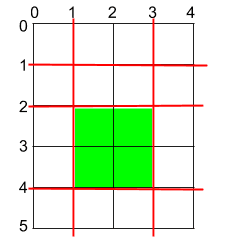
• Input: h = 5, w = 4, horizontalCuts = [1, 2, 4], verticalCuts = [1, 3]
• Output: 4
• Explanation: The figure represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.

Example 2

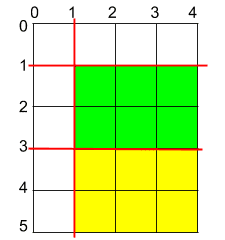
• Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
• Output: 6
• Explanation: The figure represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.

Example 3

• Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
• Output: 9

Approach: Sorting

Analysis

As seen in the figure above each horizontal cut cuts all the vertical cuts and form rectangles. Thus, the maximum area (cross-section) of the rectangle would be formed by maximum gap between horizontal cuts and vertical cuts.

To find the consecutive gaps, we need to first sort horizontalCuts and verticalCuts. In the following implementation, getMaxGap is used to find the maximum gap between the cuts (horizontal and vertical).

• First, we sort the cuts array and then assign maxGap to cuts[0] (difference between start and first cut).
• We then iterate through the array and find the maximum gap between subsequent cuts.
• Finally, we calculate the gap between last cut and end, and if it is greater than maxGap, we assign maxGap to this value.

getMaxGap is called for both horizontalCuts and verticalCuts, and we find the maximum area by multiplying the returned results.

Implementation

In C++:

int getMaxGap(vector<int> &cuts, int length) {
    sort(cuts.begin(), cuts.end());
    // gap between start (0) and first cut
    int maxGap = cuts[0];
    for (int i = 1; i < (int)cuts.size(); ++i) {
        // gap between subsequent cuts
        maxGap = max(maxGap, cuts[i] - cuts[i - 1]);
    }
    // gap between last cut and end
    maxGap = max(maxGap, length - cuts.back());
    return maxGap;
}
int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
    const int mod = 1'000'000'007;
    const int x = getMaxGap(horizontalCuts, h);
    const int y = getMaxGap(verticalCuts, w);
    return (int)((long) x % mod * (long) y % mod) % mod;
}

In Python:

def getMaxGap(cuts, length):
    cuts.sort()
    # gap between start (0) and first cut
    maxGap = cuts[0]
    for i in range(1, len(cuts)):
        # gap between subsequent cuts
        maxGap = max(maxGap, cuts[i] - cuts[i - 1])
    # gap between last cut and end
    maxGap = max(maxGap, length - cuts[-1])
    return maxGap


def maxArea(h, w, horizontalCuts, verticalCuts):
    mod = 10**9 + 7
    x = getMaxGap(horizontalCuts, h)
    y = getMaxGap(verticalCuts, w)
    return (x % mod * y % mod) % mod

Complexity Analysis

• Time Complexity: $O(NlogN + MlogM)$ required for sorting (where $N =$ len(horizontalCuts), $M =$ len(verticalCuts))
• Space Complexity: $O(1)$, constant space required