Second Largest Node in Binary Search Tree

Problem

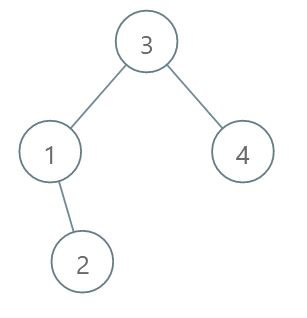
You are given the root to a binary search tree. Find the second largest node in the tree and return it. For example for the given binary search tree, return 3.

Solution

It may be noted that in the following solutions, NULL is returned if there are less than 2 nodes in the BST.

Recursive Solution

Inorder traversal traverses the BST in a sorted way. Thus, if we perform a reverse inorder traversal, we will get the largest node first and then second largest node and so on.

In the following solution k is set to 2, since we want to find the second largest node. In the reverse inorder traversal function, k is decremented every time we are at the current node (revere inorder traversal is performed by visiting right node first, then current node and then the left node). As soon as k is 0, the value of the current node is returned.

int secondLargestElement = NULL;
void reverseInorder(TreeNode* root, int &k) {
    if (root == nullptr) return;
    reverseInorder(root -> right, k);
    --k;
    if (k == 0) {
        secondLargestElement = root -> val;
        return;
    }
    reverseInorder(root -> left, k);
}

int secondLargestRecursive(TreeNode* root) {
    int k = 2;
    reverseInorder(root, k);
    return secondLargestElement;
}

• Time Complexity: $O(h)$, where $h$ is the height of the BST which can go as maximum as the number of nodes for a skewed BST.
• Space Complexity: $O(h)$ (where $h$ is the height of the BST) for the implicit stack required for recursion.

Iterative solution

For iterative solution we have to consider few cases:

• Right subtree is empty: The answer will be inorder predecessor to the root.
• Right-most node is not a leaf node: The answer will be the left child of the right most node.
• Right-most node is a leaf node: The answer will be the parent to the right-most node.

int secondLargestIterative(TreeNode* root) {
    TreeNode* prevNode;
    // empty BST
    if (!root) return NULL;
    // less than 2 nodes in the BST
    if (!root -> right and !root -> left) return NULL;
    // right subtree is empty
    if (!root -> right) {
        root = root -> left;
        while(root -> right) {
            root = root -> right;
        }
        return root -> val;
    }
    // traverse to the right most node
    while(root -> right) {
        prevNode = root;
        root = root -> right;
    }
    // empty right most node
    if (!root -> right and !root -> left) {
        return prevNode -> val;
    }
    return root -> left -> val;
}

Time Complexity: $O(h)$, where $h$ is the height of the BST which can go as maximum as the number of nodes for a skewed BST.

Space Complexity: $O(1)$.