Given the root of a binary tree, return the maximum width of the given tree.

The maximum width of a tree is the maximum width among all levels.

The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.

It is guaranteed that the answer will in the range of 32-bit signed integer.

Example 1

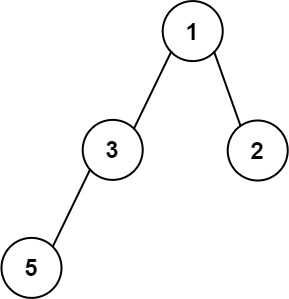
• Input: root = [1,3,2,5,3,null,9]
• Output: 4
• Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).

Example 2

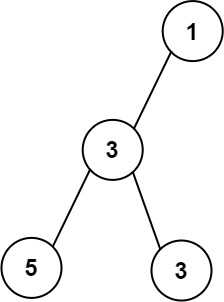
• Input: root = [1,3,null,5,3]
• Output: 2
• Explanation: The maximum width existing in the third level with the length 2 (5,3).

Example 3

• Input: root = [1,3,2,5]
• Output: 2
• Explanation: The maximum width existing in the second level with the length 2 (3,2).

Approach 1: Breadth First Search (BFS)

Idea

BFS visits the tree level by level. Thus, by modifying the BFS code we can find the width of each level of the binary tree.

We know that a binary tree can be represented by an array (assuming the root begins from the position with index 1 in the array). If the index of a node is i, the indices of its left and right children are $2i$ and $2i + 1$ respectively.

Here’s how it looks:

                1
          2               3
      4       5       6       7
    8   9   # 11    12 #     # 15

# represents a null node.

Implementation

int widthOfBinaryTree(TreeNode* root) {
    if (!root) return 0;
    long maximumWidth = 0;
    // Node, index in array
    queue<pair<TreeNode*, long>> q;
    q.push({root, 1L});
    while (!q.empty()) {
        maximumWidth = max(maximumWidth, q.back().second + 1L - q.front().second);
        int n = q.size();
        while (n--) {
            TreeNode* node = q.front().first;
            int position = q.front().second;
            q.pop();
            if (node->left) {
                q.push({node->left, position * 2L});
            }
            if (node->right) {
                q.push({node->right, position * 2L + 1L});
            }
        }
    }
    return (int)maximumWidth;
}

Complexity Analysis

• Time Complexity: $O(N)$ where $N =$ number of nodes in the binary tree
• Space Complexity: $O(N)$, at the worst case of skewed tree we will need to store all the nodes in the queue

Approach 2: Depth First Search

Idea

We can use the similar technique we have used for BFS here as well. We keep record of the positions in the depthToPosition array and use it to calculate the width.

Implementation

int dfs(TreeNode *root, int depth, unsigned long long position, vector<pair<unsigned long long, unsigned long long>> &depthToPosition){
    if(root == nullptr) return 0;
    if(depthToPosition.size() == depth){
        depthToPosition.push_back({position, position});
    } else {
        depthToPosition[depth].second = position;
    }
    int cur = depthToPosition[depth].second - depthToPosition[depth].first + 1;
    int left = dfs(root -> left, depth + 1, 2ULL * position, depthToPosition);
    int right = dfs(root -> right, depth + 1, 2ULL * position + 1ULL, depthToPosition);
    return max({cur, left, right});
}
    
int widthOfBinaryTree(TreeNode* root) {
    // records position for start and end of a level respectively
    vector<pair<unsigned long long, unsigned long long>> depthToPosition;
    return dfs(root, 0, 1ULL, depthToPosition);
}

• Time Complexity: $O(N)$ where $N =$ number of nodes in the binary tree
• Space Complexity: $O(N)$, at the worst case of skewed tree we will need to store the details of all the nodes in the recursion stack